Checknums in Banking
Or, making sure wrong transfers are detected before they are sent.
Published on 2024-11-06 | 10m 19s
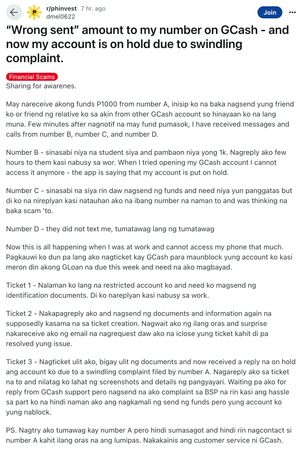
I say supposedly because there is a chance this is a scam. The modus is basically:
- Send money to a random number
- Get them to send it to you
- Get Customer Support to return it to them as well so you are out twice the amount
The only correct way to handle this is to tell the other person to contact customer support. You do not touch the money at all. There are a couple of risks if you do:
- You become part of a money laundering operation (this is called a money mule). They sent it to you to clean the money and now you are also a suspect and in a bad situation.
- You send the money to the other person but the other person also contacts customer support. CS refunds the amount to them taking money out of YOUR account to them.
Of course there's a third option which is the most likely: You send the money to the other person and you both live your lives as if nothing happened. But the risk is always there - that’s why you do not send back the money. You tell them to contact the financial institution.
But this is the Philippines and if you are the one who wrongly sent the money, there are reasons to be scared. For one, both BSP[^1] and GCash (both Cash In and Send Money) tell you to contact the person directly despite being the wrong solution. Even though there is a legal way to recover the funds, this is still too much of a hassle for the majority of wrongly sent transactions.
[^1]: Dear BSP, why can I not find this on a non-Facebook channel? And why put the text in an image? I guess blind people don't need to know about the policy?
On a personal note, these solutions are absurd - financial institutions are basically transferring the responsibility of verifying the transaction to the person. That’s why I wondered why we do not add a way to prevent wrongly sent transactions in the first place. There is already a widely accepted way to do so: Checknums.
How a Checknum works
A checknum is a number which tells you a certain number is valid. You probably have seen this in action.
If you have a credit or debit card, you know you cannot just randomly put in numbers to a website because they will tell you it is invalid. But if there are millions of millions of possible numbers, how can they tell immediately? The simple answer is that the number itself provides the information. That number is created from the Luhn Algorithm.
- Starting from the rightmost digit (the check digit), move left and double the value of every second digit. If doubling a digit results in a number greater than 9, subtract 9 from the product.
- Sum all the digits of the resulting numbers.
- Calculate the check digit by finding the smallest number that, when added to the sum, results in a multiple of 10.
Example
Let’s use the fake VISA credit card number 5555 5555 5555 4444. This is a test credit card number so don't try putting this in random websites thinking you can buy whatever you want.
Step 1: Double every other value except the last number (since that is the check digit). If the number is greater than 9, subtract 9. Since the last number is the check digit, I will remove it.
// The last number is ommitted because it is the check digit
5 5 5 5 - 5 5 5 5 - 5 5 5 5 - 4 4 4
// Double every other digit starting from the last digit
5*2 5 5*2 5 - 5*2 5 5*2 5 - 5*2 5 5*2 5 - 4*2 4 4*2
10 5 10 5 - 10 5 10 5 - 10 5 10 5 - 8 4 8
// Subtract 9 from the digits if they are greater than 9
10-9 5 10-9 5 - 10-9 5 10-9 5 - 10-9 5 10-9 5 - 8 4 8
1 5 1 5 - 1 5 1 5 - 1 5 1 5 - 8 4 8Step 2: Sum all the digits
1 + 5 + 1 + 5 + 1 + 5 + 1 + 5 + 1 + 5 + 1 + 5 + 8 + 4 + 8 = 56Step 3: Find the smallest number to add to step 2 so that it is a multiple of 10.
In our example above, the smallest number to add to 56 so it is a multiple of 10 is 4. Our check digit is thus 4. Thus, the credit card number is valid.
As you can see, if we simply randomly generated a credit card number, it wouldn’t necessarily be valid. Here is a more complex test card number from AMEX: 37144 963539 8431 (Again a test card number).
-
Resulting number from Step 1:
3 5 1 8 4 9 6 6 5 6 9 7 4 6// The last number is ommitted because it is the check digit 3 7 1 4 4 9 6 3 5 3 9 8 4 3 // Double every other digit starting from the last digit 3 7*2 1 4*2 4 9*2 6 3*2 5 3*2 9 8*2 4 3*2 3 14 1 8 4 18 6 6 5 6 9 16 4 6 // Subtract 9 from the digits if they are greater than 9 3 14-9 1 8 4 18-9 6 6 5 6 9 16-9 4 6 3 5 1 8 4 9 6 6 5 6 9 7 4 6 -
Sum all the Digits:
79 -
Missing Number:
1
Now, if someone mistypes the credit card number by using a different number or switching the numbers, the software can easily know if it’s invalid. Thus, the transaction won’t proceed. (A demo for the algorithm is shown in the Luhn Algorithm Section).
Plus, it’s still easy to generate credit card numbers - generate iteratively and then add the checknum at the end. But you still protect consumers from most mistypes.
One thing to remember though is that the checknum is NOT a security measure. It does NOT prevent someone from hacking you or creating unauthorized purchases. It simply protects against mistypes - that is all.
In other words, it protects the sender from sending to the wrong number. If this was implemented in a system, a person who "wrongly sent you funds" is most certainly lying.
Implementations of Algorithms in Python and JS
One of the reasons the checknum is so useful is because you can immediately verify if the number is valid before the transaction. You might have seen this when you entered the wrong credit card number - the site immediately tells you it is wrong. You can then double check your input and correct what is wrong.
That being said, I am a programmer and so I took up the challenge of implementing two checknum algorithms in Python and JS. One of them is the algorithm used by credit cards.
Also, you can use the code here anywhere you want - even commercially. The code license is MIT.
Luhn Algorithm
The Luhn Algorithm is the one used in credit card numbers - and it works pretty well. There are some issues with it which I’ll get to in the second algorithm but the basic steps to get the checknum is as follows:
- Double every other digit starting from the last. If the number is greater than 10, subtract 9 from the number
- Sum all the digits
- Is the number divisible by 10? If it is, it's a valid number. If you’re finding the check number, just find the smallest number that makes the number divisible by 10.
It's a pretty simple algorithm that is easy to implement. Here’s one in Python:
def is_num_valid(num: int) -> bool:
integer_digits = [int(n) for n in str(num)]
reversed_integer_digits = integer_digits[::-1]
# Remember that list indexes start at 0. So you have to check if the digit is odd
doubled_num = [n * 2 if i % 2 == 1 else n for i, n in enumerate(reversed_integer_digits)]
modified_double_num = [n - 9 if n > 10 else n for n in doubled_num]
return sum(modified_double_num) % 10 == 0
def get_checknum(num: int) -> int:
integer_digits = [int(n) for n in str(num)]
reversed_integer_digits = integer_digits[::-1]
# Since we're getting the check num, we need to start at 0
doubled_num = [n * 2 if i % 2 == 0 else n for i, n in enumerate(reversed_integer_digits)]
modified_double_num = [n - 9 if n > 10 else n for n in doubled_num]
return 10 - (sum(modified_double_num) % 10)And here’s one for JS:
function is_num_valid(num) {
const integer_digits = num
.toString()
.split("")
.map((i) => parseInt(i));
const reversed_integer_digits = integer_digits.reverse();
const doubled_num = reversed_integer_digits.map((n, i) => {
// Array Indexes start at 0. So you need to check for odd
if (i % 2 === 1) {
return n * 2;
} else {
return n;
}
});
const modified_double_num = doubled_num.map((n) => {
if (n > 10) {
return n - 9;
} else {
return n;
}
});
const sum_of_check = modified_double_num.reduce((a, b) => a + b, 0);
return sum_of_check % 10 === 0;
}
function get_checknum(num) {
const integer_digits = num
.toString()
.split("")
.map((i) => parseInt(i));
const reversed_integer_digits = integer_digits.reverse();
const doubled_num = reversed_integer_digits.map((n, i) => {
// Since we're getting the check num, we need to start at 0
if (i % 2 === 0) {
return n * 2;
} else {
return n;
}
});
const modified_double_num = doubled_num.map((n) => {
if (n > 10) {
return n - 9;
} else {
return n;
}
});
const sum_of_check = modified_double_num.reduce((a, b) => a + b, 0);
return 10 - (sum_of_check % 10);
}And here’s a demo of the algorithm:
Damm Algorithm
While the Luhn algorithm works well, if you look closely, it cannot detect certain transpositions. One of them is 09 and 90 - that means mistyping 10900 as 10090 is valid. Given that we want checknums to actually figure this out, this is not a good enough solution. One alternative is to use another checknum algorithm: the Damm Algorithm.
It requires the use of this table:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 1 | 7 | 5 | 9 | 8 | 6 | 4 | 2 |
| 1 | 7 | 0 | 9 | 2 | 1 | 5 | 4 | 8 | 6 | 3 |
| 2 | 4 | 2 | 0 | 6 | 8 | 7 | 1 | 3 | 5 | 9 |
| 3 | 1 | 7 | 5 | 0 | 9 | 8 | 3 | 4 | 2 | 6 |
| 4 | 6 | 1 | 2 | 3 | 0 | 4 | 5 | 9 | 7 | 8 |
| 5 | 3 | 6 | 7 | 4 | 2 | 0 | 9 | 5 | 8 | 1 |
| 6 | 5 | 8 | 6 | 9 | 7 | 2 | 0 | 1 | 3 | 4 |
| 7 | 8 | 9 | 4 | 5 | 3 | 6 | 2 | 0 | 1 | 7 |
| 8 | 9 | 4 | 3 | 8 | 6 | 1 | 7 | 2 | 0 | 5 |
| 9 | 2 | 5 | 8 | 1 | 4 | 3 | 6 | 7 | 9 | 0 |
To calculate the check digit, let’s take the phone number 0917 123 4567. The row indicates the previous interim number and the column indicates the current digit. If there’s a leading 0, we just skip it so let’s start with 9:
Row 0 (since we just started - this is the starting interim number), Column 9 (since the first number is 9): 2 (this is now our new interim number)
Row 2 (this is now our digit), Column 1 (we move left to right): 2
Row 2, Column 7: 3
Row 3, Column 1: 7
Row 7, Column 2: 4
Row 4, Column 3: 3
Row 3, Column 4: 9
Row 9, Column 5: 3
Row 3, Column 6: 3
Row 3, Column 7: 4
The last number is now our check number. We can verify by going to Row 7, Column 7. The result is 0 which means our number is valid. Our account number will then be 0917 123 4567 4.
If our sender somehow mistakenly entered a few numbers, it will then be invalid. Thus, financial apps can tell the sender to check it again and prevent a wrong send.
As promised, here is the implementation in Python:
def is_num_valid(num: int) -> bool:
damm_table = [
[0, 3, 1, 7, 5, 9, 8, 6, 4, 2],
[7, 0, 9, 2, 1, 5, 4, 8, 6, 3],
[4, 2, 0, 6, 8, 7, 1, 3, 5, 9],
[1, 7, 5, 0, 9, 8, 3, 4, 2, 6],
[6, 1, 2, 3, 0, 4, 5, 9, 7, 8],
[3, 6, 7, 4, 2, 0, 9, 5, 8, 1],
[5, 8, 6, 9, 7, 2, 0, 1, 3, 4],
[8, 9, 4, 5, 3, 6, 2, 0, 1, 7],
[9, 4, 3, 8, 6, 1, 7, 2, 0, 5],
[2, 5, 8, 1, 4, 3, 6, 7, 9, 0],
]
integer_digits = [int(n) for n in str(num)]
interim_digit = 0
for n in integer_digits:
interim_digit = damm_table[interim_digit][n]
return interim_digit == 0
def get_checknum(num: int) -> int:
damm_table = [
[0, 3, 1, 7, 5, 9, 8, 6, 4, 2],
[7, 0, 9, 2, 1, 5, 4, 8, 6, 3],
[4, 2, 0, 6, 8, 7, 1, 3, 5, 9],
[1, 7, 5, 0, 9, 8, 3, 4, 2, 6],
[6, 1, 2, 3, 0, 4, 5, 9, 7, 8],
[3, 6, 7, 4, 2, 0, 9, 5, 8, 1],
[5, 8, 6, 9, 7, 2, 0, 1, 3, 4],
[8, 9, 4, 5, 3, 6, 2, 0, 1, 7],
[9, 4, 3, 8, 6, 1, 7, 2, 0, 5],
[2, 5, 8, 1, 4, 3, 6, 7, 9, 0],
]
integer_digits = [int(n) for n in str(num)]
interim_digit = 0
for n in integer_digits:
interim_digit = damm_table[interim_digit][n]
return interim_digitAnd here is the one in JS:
function is_num_valid(num) {
const damm_table = [
[0, 3, 1, 7, 5, 9, 8, 6, 4, 2],
[7, 0, 9, 2, 1, 5, 4, 8, 6, 3],
[4, 2, 0, 6, 8, 7, 1, 3, 5, 9],
[1, 7, 5, 0, 9, 8, 3, 4, 2, 6],
[6, 1, 2, 3, 0, 4, 5, 9, 7, 8],
[3, 6, 7, 4, 2, 0, 9, 5, 8, 1],
[5, 8, 6, 9, 7, 2, 0, 1, 3, 4],
[8, 9, 4, 5, 3, 6, 2, 0, 1, 7],
[9, 4, 3, 8, 6, 1, 7, 2, 0, 5],
[2, 5, 8, 1, 4, 3, 6, 7, 9, 0],
];
const integer_digits = num
.toString()
.split("")
.map((i) => parseInt(i));
let interim_digit = 0;
for (const n of integer_digits) {
interim_digit = damm_table[interim_digit][n];
}
return interim_digit === 0;
}
function get_checknum(num) {
const damm_table = [
[0, 3, 1, 7, 5, 9, 8, 6, 4, 2],
[7, 0, 9, 2, 1, 5, 4, 8, 6, 3],
[4, 2, 0, 6, 8, 7, 1, 3, 5, 9],
[1, 7, 5, 0, 9, 8, 3, 4, 2, 6],
[6, 1, 2, 3, 0, 4, 5, 9, 7, 8],
[3, 6, 7, 4, 2, 0, 9, 5, 8, 1],
[5, 8, 6, 9, 7, 2, 0, 1, 3, 4],
[8, 9, 4, 5, 3, 6, 2, 0, 1, 7],
[9, 4, 3, 8, 6, 1, 7, 2, 0, 5],
[2, 5, 8, 1, 4, 3, 6, 7, 9, 0],
];
const integer_digits = num
.toString()
.split("")
.map((i) => parseInt(i));
let interim_digit = 0;
for (const n of integer_digits) {
interim_digit = damm_table[interim_digit][n];
}
return interim_digit;
}Conclusion
As a personal note, I really dislike the use of mobile phone numbers as a bank account number for many electronic wallets. People use this for communicating with other people and not everyone is comfortable giving it out just to receive money - myself included.
The BSP has tried to solve this with QR codes which is a good step but I really hope that we move to a different solution once their goals of financial inclusion are met (which I personally commend them for). People should be able to expect the best from financial institutions.